La théorie constructale

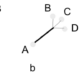
La théorie constructale, proposée par Adrian Béjan [2000] explique l’émergence des formes, notamment des réseaux, par le principe d’optimisation des flux. Soit un flux devant s’écouler d’un point A au point B [figure 1a] (voir schéma joint). Le tube est la forme qui permet la circulation la plus rapide car la plus directe. Si le flux doit aller d’un point A aux trois points B, C et D, la circulation la plus efficace est obtenue avec la forme de la figure 1b. Ce principe se répète à tous les niveaux. Une configuration à petite échelle est l’assemblage hiérarchique de ces formes élémentaires. Un réseau fluvial répète à tous les niveaux, du ruisselet au fleuve qui atteint la mer en un point, une même arborescence [figure 1c]. Toutes les formes se construisent par agrégation de ces briques élémentaires, d’où le terme de constructale retenu par A. Béjan.
Les formes réelles s’écartent en partie de ce schéma, car aucun flux ne circule dans le vide. Tout flux traverse un milieu. Les contraintes variées, très différentes suivant le flux considéré, l’eau dans un bassin versant, le sang dans un corps, des migrants pendulaires dans un tissu urbain, sont cependant toutes assimilables à un champ de friction qui tend à s’opposer, à ralentir et parfois détourner le flux. Ce couple flux-friction engendre des réseaux hiérarchiques.

Suivant le phénomène géographique étudié, l’optimisation concerne des variables différentes. Pour un réseau hydrographique, l’optimisation consistera à maximiser la masse d’eau transportée par unité de temps ou par unité d’énergie. Et pour un réseau de transport urbain, l’optimisation visera à maximiser la vitesse des déplacements ou le nombre de passagers par unité de temps ou d’énergie. Un optimum est relatif à un contexte et dépend de l’objectif que se fixe le modélisateur [Maignant, 2009]. De ce fait l’optimum n’est pas obligatoirement la situation la meilleure en termes sociaux. Ce principe d’optimisation, est un exemple du principe de moindre action, appelé aussi principe variationnel par les physiciens contemporains.

Ce type de raisonnement guidait déjà les travaux conduits par d’Arcy Thompson sur l’évolution des formes biologiques. Mais, pour ce biologiste, l’optimisation des formes était l’œuvre des forces physiques. Pour A. Béjan, l’optimisation des formes est plutôt d’origine énergétique. Pour qu’un système se maintienne, il doit évoluer de manière à permettre une circulation facile, une circulation optimale des flux qui le traversent. La forme émerge pour répondre à ce principe d’optimisation. Et la forme évolue toujours pour améliorer la circulation des flux. Ce sont les flux, le mouvement qui produit des formes. Quand le flux est assez rapide, la turbulence devient la meilleure façon de transférer la matière ou l’information. Ainsi, la théorie d’A. Béjan rend compte de l’interdépendance entre réseau et territoire. Il n’y a pas d’une part un réseau et d’autre part un territoire. Les formes territoriales dépendent des réseaux, et inversement la configuration d’un réseau dépend du territoire, des frictions qu’il impose à la circulation optimale d’un type de flux.

Cette théorie explique très bien la formation de réseaux hiérarchisés fractals [Dauphiné, 2012]. Elle est encore invoquée pour comprendre la formation des cellules de circulation atmosphérique à l’échelle du globe, l’organisation fractale des rues en ville, des réseaux de rivières, la structure granulaire des plages mais aussi les lois d’invariance d’échelle qui relient la vitesse de déplacements à la forme du corps de tous les animaux. Dans un ouvrage récent, A. Béjan [2012] montre que ce même principe s’applique aux phénomènes sociaux. Une société est assimilée à un ensemble de flux de matières, d’idées, d’énergies et d’informations. Qu’il s’agisse de l’armée ou de tout autre entreprise, pour optimiser les flux dans des systèmes point-surface ou surface-point [figure 1c], se mettent en place des réseaux hiérarchiques. Ainsi, l’organisation hiérarchique émerge « naturellement » car elle est la plus efficace pour transporter un flux d’argent, de pouvoir ou même d’idées.

Peu connue en géographie, la théorie constructale devrait inspirer les spécialistes de l’aménagement du territoire, car ils consacrent beaucoup d’efforts à tous les axes de transport et de communication. En outre, ils doivent penser le territoire en termes d’optimisation et d’équité. Des études existent pour dimensionner les réseaux d’eau potable. La plus originale concerne les structures de collecte des déchets. Leurs auteurs démontrent que pour diminuer les coûts en diminuant le temps de collecte, un modèle de collecte constructale à trois niveaux, travailleurs, transport le long d’une rue par un petit engin, puis regroupement dans de volumineux camions, serait plus efficace que le modèle de collecte traditionnelle, faisant circuler des camions identiques de même taille dans toutes les ruelles et larges avenues. Au-delà de ces applications pratiques, cette théorie a pour ambition de compléter, voire pour certains de remplacer, les théories qui expliquent la morphogenèse par les seules fonctions.

Quelles que soient ses limites, encore mal perçues, cette théorie participe au renouveau des sciences morphologiques. Parmi ces limites, il n’est pas certain que le principe d’optimisation s’applique à toutes les activités humaines. On retrouve une limite déjà présente dans les modèles de von Thünen et de Christaller. De plus, la théorie constructale ne permet sans doute pas de comprendre toutes les irrégularités d’une forme fractale, mais elle rend bien compte de sa structure d’ensemble et de son évolution. Ainsi, cette théorie donne un nouvel éclairage de l’organisation aréolaire, mais en même temps dirigée par des axes de transport, de l’étalement urbain.

André Dauphiné