Diffusion spatiale

La diffusion est à la fois l’action, et le résultat de l’action, de se répandre, ou de transmettre et de propager de manière uniforme. Elle s’exprime donc par tous les déplacements qui, quelle qu’en soit la force motrice, cherchent a répandre quelque chose de manière homogène dans un «système», tendant ainsi à le faire passer d’un état d’équilibre à un autre état d’équilibre quand, sous des conditions données, le système est saturé, ses capacités d’absorption ayant été épuisées. La notion de diffusion, prise au sens de l’action, est introduite quand on étudie des «processus» qui mettent en jeu des déplacements de matière, de produits, de personnes, de pratiques, ou d’idées dans ensemble. La notion de diffusion spatiale recouvre l’ensemble des processus qui concourent au déplacement, à la migration dans l’espace géographique, et aux effets en retour que ces déplacements engendrent dans cet espace. La diffusion peut correspondre à un mouvement de migration avec re-localisation ou à un mouvement d’expansion

Tout déplacement dans l’espace peut-il être assimilé à une diffusion ? On considère en général que si le déplacement aboutit à une forme de colonisation, à une implantation, à une installation de quelque chose de nouveau dont la complexité est suffisante pour que la force intégratrice soit prévisible à différents échelons géographiques, l’assimilation est acceptable.

Une approche nomothétique de la diffusion spatiale est véritablement introduite en géographie par T. Hägerstrand (1952) qui, à partir de plusieurs études de cas, met en évidence l’existence de régularités temporelles et spatiales dans les processus de diffusion spatiale des innovations. L’énoncé de ces régularités a ouvert la voie à leur «modélisation», et relancé la réflexion sur leur rôle dans la «dynamique» des espaces géographiques.

Des conditions nécessaires pour que se produise la diffusion spatiale d’une innovation ont ainsi été identifiées :

• apparition en un «lieu» d’une innovation apte au déplacement et qui puisse s’imposer en tant que telle
• capacité du lieu d’apparition de l’innovation à devenir foyer émetteur
• existence d’un «milieu» d’accueil qui favorise une propagation rapide
• force de propagation suffisamment grande et temps de propagation suffisamment long pour que l’interruption du processus de diffusion soit peu probable.

La diffusion spatiale privilégie certains canaux de propagation. Elle procède largement par contagion dans le «voisinage» : les probabilités de contact entre émetteurs et récepteurs de l’innovation diminuant rapidement avec la distance. Elle est particulièrement sensible à la structure hiérarchique des systèmes de peuplement, le phénomène nouveau a tendance à apparaître en suivant le sens descendant de la «hiérarchie» urbaine. Enfin, et pour les mêmes raisons, plus le centre émetteur est grand, plus sa force d’impulsion dans le processus de diffusion est élevée, d’où le sens descendant de la diffusion d’un très grand nombre d’innovations dans les «réseaux» urbains. A l’inverse les processus de diffusion spatiale des innovations sont freinés, déviés, parfois arrêtés par les barrières spatiales. Enfin, un même processus de diffusion spatiale est le plus souvent multiscalaire, et dans ce cas, le jeu des «interactions» qui guide la diffusion se modifie d’un échelon géographique à un autre.

L’inscription de la diffusion spatiale dans le temps obéit à certaines règles. L’étape primaire du processus correspond à l’amorce de la diffusion. A ce stade, la diffusion introduit une différenciation nouvelle dans l’espace géographique, un contraste entre les lieux qui ont adopté l’innovation et les autres lieux se dessine. L’étape d’expansion est la période de développement proprement dit du processus, qui se traduit par une réduction progressive des plus forts contrastes entre lieux. Durant l’étape suivante dite de condensation, le taux de pénétration dans les différents lieux tend à s’homogénéiser, cependant que, d’un lieu à un autre, les vitesses de diffusion se rapprochent. L’étape ultime du processus, dite étape de saturation est celle au cours de laquelle le taux de pénétration de l’innovation croît de manière asymptotique vers un maximum.

L’apparente instantanéité de la propagation, permise par de nouvelles techniques de diffusion de l’information, accrédite parfois l’idée que les décalages spatio-temporels de la diffusion auraient perdu toute signification. Si, pour un grand nombre d’innovations, ces nouvelles techniques ont probablement réduit les frictions du temps et de la distance dans la transmission de l’information, les structures de l’espace géographique d’accueil maintiennent des différentiels importants dans les temps de réponse qui transforment une information reçue en une innovation adoptée.

En sciences sociales, la notion de diffusion est en général associée à celle d’innovation. Innover c’est introduire dans une chose établie quelque chose de nouveau, d’encore inconnu, qui est de nature à transformer celle-ci. L’innovation est indissociable de la diffusion. Ne se réduisant ni à l’invention, ni à la mode, elle est, au sens donné par Schumpeter (1934), la combinaison de choses nouvelles qui, se propageant dans un milieu, engendrent des irréversibilités dans l’évolution de ce milieu. Plus l’innovation diffusée est complexe, plus le processus de sa diffusion aura d’influence sur la transformation du milieu de sa propagation, car plus les effets induits par son adoption sont démultipliés

Les processus de diffusion spatiale des innovations sont modélisables. Les tentatives faites en ce sens ont été très nombreuses, en particulier chez les géographes, les épidémiologues, les démographes et les botanistes.

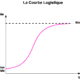
• Une fonction logistique, qui décrit la croissance d’une population dans un espace aux ressources limitées, est communément utilisée pour modéliser le développement du processus dans le temps, le nombre des adoptants potentiels représentant la ressource qui limite l’expansion de la diffusion. Les quatre grandes étapes du processus de diffusion peuvent être repérées sur la courbe qui représente cette fonction.
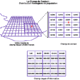
• La modélisation de la dimension spatiale du processus de la diffusion mobilise les principes de base mis en oeuvre dans les modèles d’interaction spatiale (effet des masses, et de la distance, effets de barrière, etc..), auxquels on donne assez souvent la forme d’une fonction exponentielle négative de la distance. Le temps du processus étant discrétisé, à chaque unité de temps, les règles d’interaction spatiale introduites dans le modèle, permettent de définir en tout lieu les probabilités de contact entre émetteur et récepteur et donc les probabilités de propagation locale (champ de contact exprimé en grille de probabilités). De nombreuses sophistications sont intervenues pour tenir compte en particulier de conditions locales de propagation, aux côtés des conditions générales dont est censé rendre compte le champ de contact. T.Hägerstrand (1953) avait préconisé le recours à la méthode Monte Carlo pour simuler la propagation spatiale au cours du temps comme un processus aléatoire. Les méthodes informatiques de modélisation semblent devoir beaucoup élargir le champ des possibles pour la prévision géographique d’une diffusion.